Acrobat Printable Version

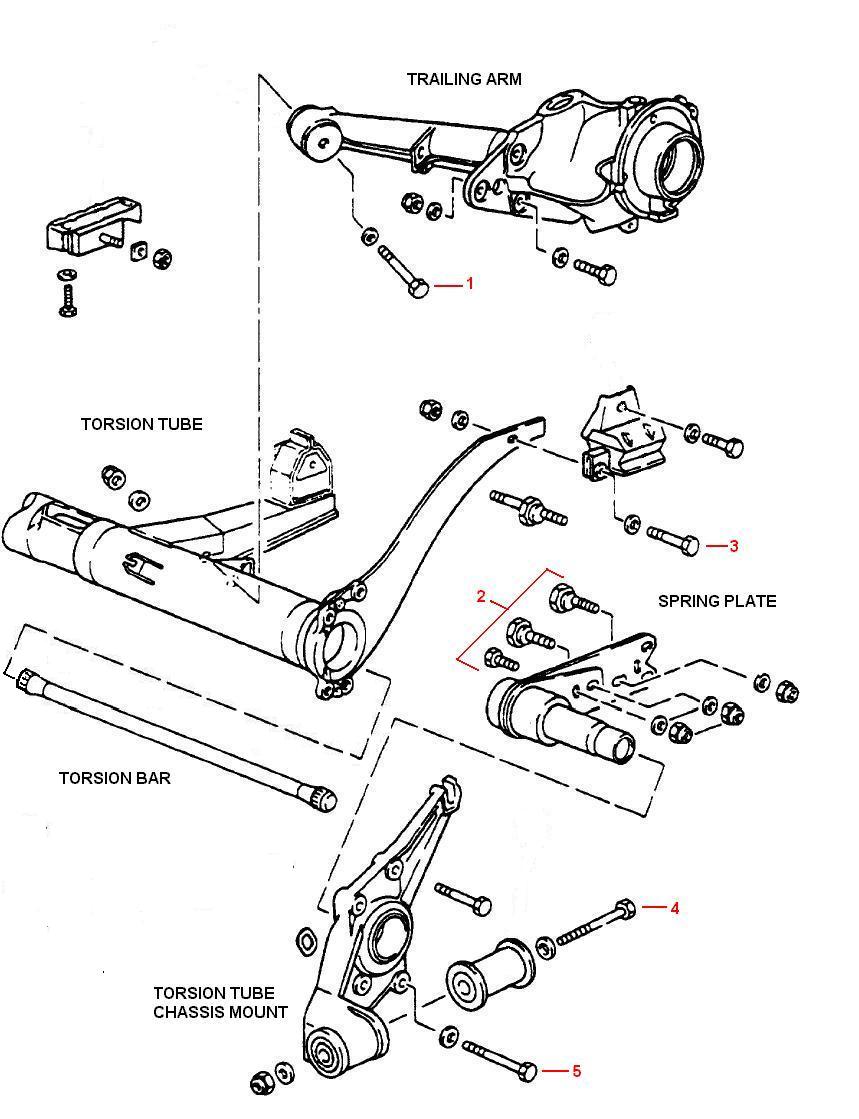
Replacing the torsion bar on a 944 is not all that difficult. However, reindexing the torsion after completion is a pain and can be very time consuming. There are a couple of reasons for removing the torsion bars. The first is to make a ride height adjustment and the second is to upgrade to a stiffer torsion bar. I was fortunate enough to come across a very good torsion bar replacement procedure written by Marc Belanger to use as a guide. The following procedure is based on my own experience and the shared experiences of Marc, Doug Donsbach, and others. These combined experiences should provide you with a pretty clear picture of what it takes to remove, replace, and reindex the torsion bars in your car. I'll also be adding some pictures to help guide you along the way. Refer to the diagram below for location of the major components and fasteners for the rear suspension.

First off, if you think you need to make a change in ride height, you first need to take a ride height measurement and determine how much of a change is needed. Typically, the best place to take a ride height measurement is from the ground up to the top-center of the fender well (i.e. centered on the wheel). A good number to use for ride height measurement at that point is about 25 inches (63,5 cm). It's really not a great idea to go much lower than that. And, you'll achieve the best results if you keep the same ride height front-to-rear. If you determine that a change in ride height is in order, a small amount of adjustment is available via the eccentric bolt on the trailing arm spring plate. The amount of adjustment available depends on where the eccentric is set to begin with. The total adjustment range is approximately 1 inch (2,5 cm). Assuming the eccentric is centered (seldom the case), you'll only be able to raise or lower the ride height by about 1/2 inch.

Tools

• Jack Stands and Floor Jack
• Metric Socket and Combination Wrench Set
• Pry bar

Other Procedures Needed

• SUSP-05, Rear Sway Bar Removal and Installation

NOTE

You should have already determined the pre-existing ride height as described in the introduction section.

NOTE

If you are simply reindexing existing torsion bars, proceed to Step 6. Steps 1-5 are only required when installing different torsion bars.

1. Raise the rear of the vehicle.
2. Using SUSP-05, remove the rear sway bar and drop links.
3. Lower the vehicle back to the ground and bounce the rear of the car several times to get the suspension to settle.
4. Fabricate a measuring device similar to the one show in the figure below to allow measurement of the position of the spring plate in relation to the torsion tube chassis mount (end cap). I believe Doug Donsbach originally came up with this idea. Basically, the device has two holes that correspond to the bottom two bolts on the end cap to give a point of reference.
   

5. With the vehicle sitting on the ground, measure the height of the spring plate in relation to the torsion tube end cap and mark the position on the measuring device (see below). This is the loaded spring plate height. This will be a bit awkward with the wheel in place and the car sitting on the ground.
   

6. Raise the rear of the vehicle and place it on jack stands.
7. Remove the rear wheels.
8. Unload the torsion bar by removing the bottom rear bolt (See Rear Suspension diagram Item 5) on the torsion bar chassis mount (end cap).
9. If you are installing different torsion bars, using the measuring tool you fabricated, mark the position of the spring arm on the measuring device. This is the unloaded spring arm position.
   

10. Disconnect the rear brake lines at the calipers.
11. Unplug the brake pad wear sensors.
12. Unbolt and disconnect both rear axles from their trailing arms. Hang them out of the way using bungie cords or wire.
13. Remove the bolt that attaches the trailing arm to the torsion tube bolt (See Rear Suspension diagram Item 1 - one bolt on each trailing arm).
14. Support the trailing arms from the transmission crossmember using a heavy duty strap. A good quality strap is called for as the trailing arm and rotor assembly is fairly heavy . It will become damaged, damage other components, or worse yet, injure you if it is not properly supported. The trailing arm assembly will be hanging freely when the spring plate bolts are removed in the next step.
15. Remove the nuts and bolts that hold the trailing arm to the spring plate (See Rear Suspension diagram Item 2 - three nuts and bolts on each trailing arm). Note that the back two bolts are eccentric bolts used to adjust the height of the trailing arm. You may have to tap on the end of the eccentric bolt where the retaining nut was removed to free it from the spring plate.
16. Remove the nut and bolt that holds the torsion tube cantilever arm to the chassis mount near the top of the wheel well (See Rear Suspension diagram Item 3 - one bolt and nut on each trailing arm).
17. Place the floor jack underneath the center of the torsion tube assembly. Raise the jack until it just contacts the torsion tube assembly.
18. Remove the nut and bolt that attaches the torsion tube chassis mount to the body of the vehicle (See Rear Suspension diagram Item 4 - one nut and bolt on each trailing arm chassis mount).
    

19. Gently pry on the torsion tube assembly, alternating sides, until the assembly is free from the body. Lower the assembly on the floor jack far enough to slide the torsion bar out of the torsion tube once the torsion tube assembly chassis mounts and spring plates are removed.
20. The torsion tube chassis mount has four bolts which attach it to the torsion tube.
21. Remove the remaining three bolts in the torsion tube chassis mount.
22. Remove the torsion tube chassis mount and spring plate.
23. Pull the torsion bar out of the torsion tube.

Replacing

1. Determine the old torsion bar loaded-to-unloaded range on the measuring device which you fabricated during the torsion bar removal (distance between the two marks).
   
   NOTE

   If you are replacing a solid torsion bar with a hollow torsion bar, the manufacturer should supply a solid diameter that the hollow bar is equivalent to. Use the solid bar equivalent diameter in the calculation below.

2. Calculate the new torsion bar loaded-to-unloaded range using the formula below:

      Example:
   
   
      Let's assume you currently have 25.5mm torsion bars and want to swap
      to 30mm bars and that the loaded-to-unloaded range on your old bar is 
      50mm. The loaded-to-unloaded range for your new bar would be 
      calculated as follows:
   
   
      
   
   

3. Using the loaded-to-unloaded range for the new bar, measure that distance down from the loaded mark (top mark) on your measuring device and make a mark on the device at that point. This is the new bar unloaded position.
4. Install the new torsion bar into the torsion tube.
5. Install the spring plate and torsion tube end cap on to the torsion tube. Use the measuring device to check that the spring plate is aligned to the new bar unloaded position when installing the spring plate.
6. Install at least two bolts into the end cap to hold it in position while the ride height is being checked.
7. When both torsion bars have been replaced, raise the torsion tube assembly into position using the floor jack.
8. Bolt the trailing arms to the spring plates ensuring the eccentric adjusting bolt is centered.
9. Bolt the trailing arm to the torsion tube.
10. Attach the torsion tube cantilever arm to the chassis mount near the top of the wheel well.
11. Attach the torsion tube chassis mount (end cap) to the chassis.
12. Remove the vehicle from the jack stands, bounce the rear end of the car several times, and check the ride height.
13. If the ride height needs adjusting and it is with ± 1/2", adjust the eccentric bolt on the spring plate to obtain the desired ride height.
14. If the needed ride height adjustment is greater than 1/2", unbolt and lower the torsion bar assembly, reindex the torsion bars as described in the section that follows, reinstall the assembly, and check the ride height again. Repeat this as necessary until the correct ride height is obtained. Do not be surprised if it takes you three or more times to achieve the correct right height. This is very common. Also, do not be surprised if you have to reindex the bars several days after completion once everything has had a chance to settle completely.
15. Once the correct ride height is obtained, complete the reassembly by installing any remaining bolts in the torsion tube end caps and installing the rear sway bar.

Indexing the torsion bars on a 944 is tedious at best, but fortunately it isn't rocket science. However, after the following explanation of how torsion bar indexing works it may seem like rocket science.

If you've never studied geometry, this may completely new to you. However, bear with me and we will ultimately arrive at some formulas you will be able to use regardless of whether you understand circular geometry. First, we have to understand that in geometry a circle is divided into increments called degrees (°) and that there are 360 degrees in a complete circle. Each degree is divided into increments called minutes and there are 60 minutes (') in each degree.

Now, if you examine a 944 torsion bar, you'll find that the inner end of the torsion bar has 40 splines and the outer end of the bar has 44 splines. So, if we take the number of degrees in a circle and divide it by the number of splines, will find the amount of rotation that can be obtained by moving the bar 1 spline.

For the inner torsion bar end:

For the outer torsion bar end:

The measured length of the trailing arm on a 944 is 16.5" from the center of the torsion bar out to the center of the hub. Since we now know the length of the trailing arm and the number of degrees of rotation for each tooth of spline movement, we can now use fairly simple geometry for right triangles to calculate the change in ride height with each change in spline position.

Using the formulas for right triangles below, we can calculate the change in ride height (X₁).

Where:

   A = Length of Side adjacent to angle theta (θ)

   O = Length of Side opposite angle 

   H = Length of the Hypotenuse

Now for the part that may be a little harder to follow. This calculation is based on the assumption that we are dealing with a perfect right triangle. And, if you've ever studied geometry, you'll remember that the longest side of a right triangle is the hypotenuse. In our case with the trailing arm, the hypotenuse is simply the trailing arm moved from one position to another. Since the change in ride height calculation is based on the end of the trailing arm dropping straight down at a right angle from it's original position, our calculation is somewhat flawed. In reality, the hub end of the trailing arm swings along the arc of a circle. For it to drop straight down at a right angle from it's original position, the trailing arm would have to change length and we know that isn't possible. Unless, if course, Porsche comes up with something similar to Variocam for the suspension system. Anyway, we can still use the right triangle rules to come up with the actual ride height change if we do a few more calculations.

If we calculate the length of the hypotenuse at any given angle theta, that will give us the theoretical length that the trailing arm would have to lengthen to in order to maintain our right triangle. Then, we can use the difference between the theoretical trailing arm length and the actual length to form a new (smaller) right triangle which will allow us to determine the error introduced into our original calculation. I know that's hard to visualize but, bear with me.

So, let's first calculate the length of the hypotenuse (X₂) given that angle θ = 9° or one tooth on the inner torsion bar spline:

If we take the difference between the hypotenuse length at angle θ and the actual trailing arm length, we obtain a length (X₃) which we can use as the hypotenuse of a new (smaller) triangle.

And finally, we can calculate the actual change in ride height (X₅) for inner spline movement by subtracting the error (X₄) from the original ride height change (X₁):

This is approximately 6.6 cm of change in ride height. Using the same calculations and substituting in 8.18° for angle θ, we obtain the actual ride height change for a single spline rotation on the outer torsion bar splines.

That's roughly 6 cm.

Now that we know just how much or a change in ride will occur per spline on each end of the torsion bar, let's take a look at a specific example. Assume we're standing beside the driver's side of the car looking at the torsion bar end and spring plate (see picture below).

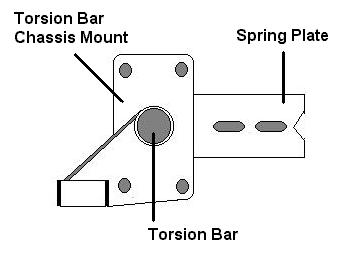
If we leave the spring plate and chassis mount attached to the outer end of the torsion bar and rotate the inner end of the bar one spline in the counter-clockwise direction, it will raise the end of the spring plate. This will lower the ride height of the car by 2.58". Then if we leave the inner end fixed in the torsion tube and rotate the spring plate and chassis mount one spline in the clockwise direction it will lower the end of the spring plate and raise the ride height of the car by 2.35". The net result will be that the car is 0.23" lower (or approximately 6mm).

Clark's Garage © 1998